|
| Fluxul de Stiri dupa Data Aparitiei |
|
Comentarii Adauga Comentariu _ Prins în mijloc: Biliardul cu cadru de memorie duce la întrebări matematice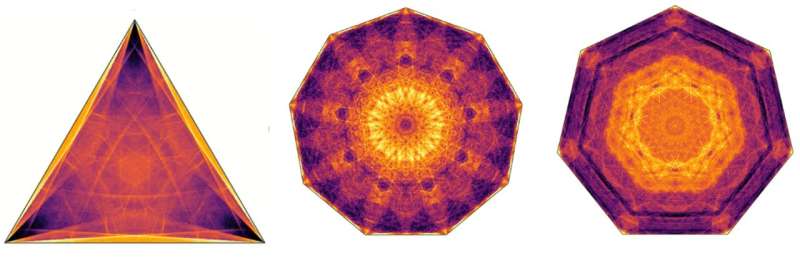 _ Prins în mijloc : Biliardul cu cadru de memorie duce la întrebări matematiceAdăugarea unei reguli simple la un joc idealizat de biliard duce la o mulțime de întrebări matematice interesante, precum și la aplicații în fizica organismelor vii. Săptămâna aceasta, cercetătorii de la Universitatea din Amsterdam, inclusiv doi masteranzi ca primi autori, au publicat o lucrare în Physical Review Letters despre dinamica fascinantă a biliardului cu memorie. O versiune idealizată a jocului de biliardul i-a fascinat pe matematicieni de zeci de ani. Întrebarea de bază este una simplă: odată ce o minge de biliard este jucată, unde se duce și unde ajunge? Să presupunem că biliardul este perfect: pereții sunt perfect săriți, nu există alte obiecte pe masă, mișcarea mingii este fără frecare și așa mai departe. Atunci mingea nu se va „termina” cu adevărat nicăieri; va continua pentru totdeauna. Dar se întoarce vreodată acolo unde a început? În cele din urmă vizitează fiecare parte a mesei? Când schimbăm ușor direcția mingii sau locația de pornire, calea pe care o urmează arată ca cea anterioară? Toate aceste întrebări se dovedesc a fi foarte interesante din punct de vedere matematic. Răspunsurile lor nu sunt întotdeauna cunoscute – mai ales când forma biliardului nu este simplă, ca un pătrat sau un dreptunghi. De exemplu, la biliardul triunghiular cu colțuri mai mici de 100 de grade, se știe că există întotdeauna căi periodice — căi pe care mingea le poate urma și care se întorc pe sine. Acest lucru poate fi demonstrat matematic. Acum, schimbă unul dintre colțuri într-un unghi puțin mai mare și niciun matematician nu mai știe răspunsul. Jocurile de biliard idealizate nu sunt doar o distracție preferată a matematicienilor. Ele au, de asemenea, un impact profund asupra fizicii și altor științe. Multe dintre întrebările despre biliard pot fi formulate ca întrebări despre haos: condiții inițiale similare ale unui sistem dinamic - indiferent dacă este vorba despre o minge pe o masă de biliard, o moleculă într-un gaz sau o pasăre într-un stol - conduc întotdeauna la un final similar. rezultate? În cercetările efectuate la Universitatea din Amsterdam, o echipă de fizicieni și-a dat seama că, schimbând ușor regulile jocului de biliard, numărul de aplicații în lumea reală crește și mai mult. Mazi Jalaal, coautor al publicației și șeful grupului în care s-a făcut cercetarea, explică: „În natură, multe organisme vii au o formă externă de memorie. De exemplu, lasă urme de amintit. unde au fost. Apoi pot folosi acele informații fie pentru a urma din nou același traseu, fie, de exemplu, atunci când caută mâncare, pentru a nu explora din nou aceeași regiune.” Aceasta din urmă opțiune i-a condus pe cercetători. la o idee interesantă: ce se întâmplă dacă adăugăm o regulă la jocul de biliard, și anume că mingea s-ar putea să nu-și traverseze niciodată propria cale anterioară? Rezultatul este că dimensiunea efectivă a mesei de biliard devine din ce în ce mai mică. De fapt, mingea rămâne în cele din urmă prinsă de propria sa traiectorie. Noi întrebări interesante Efectul de prindere face sistemul și mai intrigant. Chiar și întrebările simple devin acum extrem de fascinante. Cât de departe parcurge o minge înainte de a fi prinsă? Răspunsul variază, atât în funcție de forma mesei, cât și de punctul de plecare și direcția mingii. Uneori, mingea parcurge o lungime care este doar de câteva ori mai mare decât cea a mesei, uneori poate du-te de 100 de ori acea lungime înainte de a rămâne prins. În cazul în care mingea ajunge în cele din urmă în starea sa prinsă este, de asemenea, o întrebare complicată; repetarea experimentului pe un computer de milioane de ori, de fiecare dată cu o poziție de pornire și o viteză ușor diferite, duce la modele frumoase de configurații finale. Imaginea din partea de sus a acestui text arată câteva dintre aceste exemple frumoase. Interesant este că sistemele dinamice rezultate pot fi haotice. Schimbarea poziției de pornire sau a vitezei mingii care se evită doar puțin poate duce la prinsă într-un punct complet diferit al biliardului. În plus, spre deosebire de ceea ce se întâmplă la o masă de biliard obișnuită, eul -evitarea mingii nu este la fel de probabil să ajungă oriunde. Unele regiuni sunt mai probabile decât altele. Pentru a explica și a dovedi toate aceste caracteristici, matematicienii au cu siguranță treaba. O particularitate interesantă a publicației este că ambii primii autori sunt studenți de master. Jalaal adaugă: „Ideea unui „biliard cu memorie” este suficient de simplă și suficient de nouă încât studierea acestuia nu necesită ani de experiență. Thijs și Stijn au făcut o treabă grozavă în a-și face materialul propriu și în găsirea unor modalități inteligente de a studia toate acestea. noi probleme deschise. Sunt foarte fericit că ei pot fi deja autori principali ai unei publicații.” Rezultatele sunt doar primii pași în ceea ce ar putea fi un domeniu complet nou de cercetare. Nu numai că există multe întrebări matematice interesante care așteaptă acum să primească răspuns; aplicațiile în fizică, inclusiv biofizica, sunt, de asemenea, nesfârșite. Jalaal spune: „Conceptul de capcană este unul care cere să fie explorat, de asemenea, în sistemele din viața reală. De exemplu, știm că Mucegaiurile celulare de slime folosesc căi de autoevitare. De asemenea, rămân prinse și ce se întâmplă atunci când o fac? Sau au mecanisme inteligente pentru a evita deloc acest lucru? Îl folosesc pentru a îmbunătăți strategiile de căutare a alimentelor? „Rezultatele ne-ar ajuta să înțelegem mai bine aceste sisteme biologice și poate chiar să încorporăm lecțiile pe care le învățăm pentru a optimiza această formă de biliard cu memorie pentru utilizare la roboți.”
Linkul direct catre PetitieCitiți și cele mai căutate articole de pe Fluierul:
|
|
|
Comentarii:
Adauga Comentariu